http://www.positiveintegers.org/
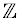 це цілком незамкнена множина без верхньої та нижньої меж. Порядок
це цілком незамкнена множина без верхньої та нижньої меж. Порядок 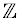 дано
... <-2 <-1 <0 <1 <2 <...
дано
... <-2 <-1 <0 <1 <2 <...
Алгебраїчні властивості цілих чисел
Подібно до натуральних чисел, множина цілих чисел 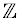 закривається під операціями додавання та множення ; тобто сума і добуток будь-яких двох цілих чисел є цілим числом. Проте з включенням від'ємних і натуральних чисел та нульовим
закривається під операціями додавання та множення ; тобто сума і добуток будь-яких двох цілих чисел є цілим числом. Проте з включенням від'ємних і натуральних чисел та нульовим 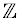 (на відміну від натуральних чисел) також закривається під віднімання . Множина цілих чисел
(на відміну від натуральних чисел) також закривається під віднімання . Множина цілих чисел 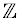 це НЕ замкнуто щодо операції ділення , так як частка від ділення двох цілих чисел (наприклад, 1 , поділене на 2), не обов'язково повинен бути цілим числом.
це НЕ замкнуто щодо операції ділення , так як частка від ділення двох цілих чисел (наприклад, 1 , поділене на 2), не обов'язково повинен бути цілим числом.
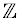 закривається під операціями додавання та множення ; тобто сума і добуток будь-яких двох цілих чисел є цілим числом. Проте з включенням від'ємних і натуральних чисел та нульовим
закривається під операціями додавання та множення ; тобто сума і добуток будь-яких двох цілих чисел є цілим числом. Проте з включенням від'ємних і натуральних чисел та нульовим 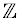 (на відміну від натуральних чисел) також закривається під віднімання . Множина цілих чисел
(на відміну від натуральних чисел) також закривається під віднімання . Множина цілих чисел 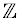 це НЕ замкнуто щодо операції ділення , так як частка від ділення двох цілих чисел (наприклад, 1 , поділене на 2), не обов'язково повинен бути цілим числом.
це НЕ замкнуто щодо операції ділення , так як частка від ділення двох цілих чисел (наприклад, 1 , поділене на 2), не обов'язково повинен бути цілим числом.
У наступній таблиці наведено деякі основні властивості додавання та множення для будь-яких цілих чисел a, b та c.
| Крім того | множення | |
| закриття : | a + b - це ціле число | a × b - ціле число |
| асоціативність : | a + (b + c) = (a + b) + c | a × (b × c) = (a × b) × c |
| комутативність : | a + b = b + a | a × b = b × a |
| наявність елемента ідентичності : | a + 0 = a | a × 1 = a |
| існування зворотних елементів : | a + (- a) = 0 | |
| дистрибутивність : | a × (b + c) = (a × b) + (a × c) | |
опис
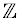 це цілком незамкнена множина без верхньої та нижньої меж. Порядок
це цілком незамкнена множина без верхньої та нижньої меж. Порядок 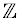 дано
дано
Ціле число додатне, якщо воно перевищує нуль, а від'ємне - менше нуля. Нульове значення визначається як ні негативний, ні позитивний номер.
Порядок цілих чисел сумісний з алгебраїчними операціями наступним чином:
- якщо <b та c <d, то a + c <b + d
- якщо <b та 0 <c, то ac <bc
дільники
Дільником цілого числа п , також званий коефіцієнт з п , являє собою ціле число , яке рівномірно ділить п , не полишаючи залишок. Якщо х - дільник n , то можна записати, що x | п . Це читається як x розділяє n . Він також зазначив , що п є ділиться на х , і що п є кратним х .
1 і -1 - дільники кожного цілого числа, а кожне ціле число - дільник 0 . Числа, розділені на 2 , називаються рівними, а ті, які не є, називаються непарними .
Назва походить від арифметичної операції поділу: якщо a / b = c, то a є дивідендом , b - дільником і c фактором .
Деякими елементарними властивостями дивізорів є:
- Якщо a | б і а | c , то a | ( b + c ).
- Якщо a | b та b | з , а потім | з .
- Якщо a | b та b | a , то a = b або a = - b .
- Граф (дефіцит) , граф (рясний) і граф (ідеальний) - це кількість дефіцитних , рясних та відмінних чисел у цьому діапазоні.
| Діапазон | кількість простих чисел (Primes) | кількість чисел (Фібоначчі) | найбільш кількість дільників (d (N))) | Числа, що мають макс. кількість дільників N | Граф (дефіцит) | Граф (рясний) | Граф (ідеальний) |
|---|---|---|---|---|---|---|---|
| 1-100 | 25 | 10 | 12 | 60, 72, 84, 90, 96 | 76 | 22 | 2 |
| 101-200 | 21 | 1 | 18 | 180 | 76 | 24 | 0 |
| 201-300 | 16 | 1 | 20 | 240 | 77 | 23 | 0 |
| 301-400 | 16 | 1 | 24 | 360 | 73 | 27 | 0 |
| 401-500 | 17 | 0 | 24 | 420, 480 | 74 | 25 | 1 |
| 501-600 | 14 | 0 | 24 | 504, 540, 600 | 76 | 24 | 0 |
| 601-700 | 16 | 1 | 24 | 630, 660, 672 | 76 | 24 | 0 |
| 701-800 | 14 | 0 | 30 | 720 | 74 | 26 | 0 |
| 801-900 | 15 | 0 | 32 | 840 | 75 | 25 | 0 |
| 901-1000 | 14 | 1 | 28 | 960 | 74 | 26 | 0 |
| 1001-1100 | 16 | 0 | 32 | 1080 | 77 | 23 | 0 |
| 1101-1200 | 12 | 0 | 30 | 1200 | 76 | 24 | 0 |
| 1201-1300 | 15 | 0 | 36 | 1260 | 76 | 24 | 0 |
| 1301-1400 рр | 11 | 0 | 32 | 1320 | 74 | 26 | 0 |
| 1401-1500 | 17 | 0 | 36 | 1440 рр | 74 | 26 | 0 |
| 1501-1600 | 12 | 1 | 32 | 1512, 1560 | 77 | 23 | 0 |
| 1601-1700 | 15 | 0 | 40 | 1680 | 74 | 26 | 0 |
| 1701-1800 | 12 | 0 | 36 | 1800 | 75 | 25 | 0 |
| 1801-1900 | 12 | 0 | 32 | 1848, 1890 | 76 | 24 | 0 |
| 1901-2000 рр | 13 | 0 | 36 | 1980 | 74 | 26 | 0 |
| 2001-2100 | 14 | 0 | 36 | 2016, 2100 | 74 | 26 | 0 |
| 2101-2200 | 10 | 0 | 40 | 2160 | 76 | 24 | 0 |
| 2201-2300 | 15 | 0 | 32 | 2280 | 75 | 25 | 0 |
| 2301-2400 | 15 | 0 | 36 | 2340, 2400 | 77 | 23 | 0 |
| 2401-2500 | 10 | 0 | 30 | 2448 | 74 | 26 | 0 |
| 2501-2600 | 11 | 1 | 48 | 2520 | 74 | 26 | 0 |
| 2601-2700 | 15 | 0 | 40 | 2640 | 78 | 22 | 0 |
| 2701-2800 | 14 | 0 | 36 | 2772 | 74 | 26 | 0 |
| 2801-2900 | 12 | 0 | 42 | 2880 | 75 | 25 | 0 |
| 2901-3000 | 11 | 0 | 36 | 2940 | 74 | 26 | 0 |
| 3001-3100 | 12 | 0 | 40 | 3024 | 76 | 24 | 0 |
| 3101-3200 | 10 | 0 | 40 | 3120 | 76 | 24 | 0 |
| 3201-3300 | 11 | 0 | 40 | 3240 | 74 | 26 | 0 |
| 3301-3400 | 15 | 0 | 48 | 3360 | 74 | 26 | 0 |
| 3401-3500 | 11 | 0 | 36 | 3420 | 74 | 26 | 0 |
| 3501-3600 | 14 | 0 | 45 | 3600 | 77 | 23 | 0 |
| 3601-3700 | 13 | 0 | 40 | 3696 | 78 | 22 | 0 |
| 3701-3800 | 12 | 0 | 48 | 3780 | 73 | 27 | 0 |
| 3801-3900 | 11 | 0 | 36 | 3840, 3900 | 74 | 26 | 0 |
| 3901-4000 | 11 | 0 | 48 | 3960 | 75 | 25 | 0 |
| 4001-4100 | 15 | 0 | 42 | 4032 | 74 | 26 | 0 |
| 4101-4200 | 9 | 1 | 48 | 4200 | 76 | 24 | 0 |
| 4201-4300 | 16 | 0 | 36 | 4284 | 74 | 26 | 0 |
| 4301-4400 | 9 | 0 | 48 | 4320 | 77 | 23 | 0 |
| 4401-4500 | 11 | 0 | 36 | 4410, 4500 | 77 | 23 | 0 |
| 4501-4600 | 12 | 0 | 40 | 4536, 4560 | 73 | 27 | 0 |
| 4601-4700 | 12 | 0 | 48 | 4620, 4680 | 74 | 26 | 0 |
| 4701-4800 | 12 | 0 | 42 | 4800 | 74 | 26 | 0 |
| 4801-4900 | 8 | 0 | 36 | 4860, 4896 | 76 | 24 | 0 |
| 4901-5000 | 15 | 0 | 36 | 4950 | 77 | 23 | 0 |
| 5001-5100 | 12 | 0 | 60 | 5040 | 75 | 25 | 0 |
| 5101-5200 | 11 | 0 | 36 | 5148 | 74 | 26 | 0 |
| 5201-5300 | 10 | 0 | 48 | 5280 | 77 | 23 | 0 |
| 5301-5400 | 10 | 0 | 48 | 5400 | 74 | 26 | 0 |
| 5401-5500 | 13 | 0 | 48 | 5460 | 75 | 25 | 0 |
| 5501-5600 | 13 | 0 | 48 | 5544 | 74 | 26 | 0 |
| 5601-5700 | 12 | 0 | 40 | 5616, 5670 | 75 | 25 | 0 |
| 5701-5800 | 10 | 0 | 48 | 5760 | 76 | 24 | 0 |
| 5801-5900 | 16 | 0 | 48 | 5880 | 73 | 27 | 0 |
| 5901-6000 | 7 | 0 | 48 | 5940 | 74 | 26 | 0 |
| 6001-6100 | 12 | 0 | 48 | 6048 | 76 | 24 | 0 |
| 6101-6200 | 11 | 0 | 48 | 6120 | 77 | 23 | 0 |
| 6201-6300 | 13 | 0 | 54 | 6300 | 72 | 28 | 0 |
| 6301-6400 | 15 | 0 | 42 | 6336 | 75 | 25 | 0 |
| 6401-6500 | 8 | 0 | 50 | 6480 | 74 | 26 | 0 |
| 6501-6600 | 11 | 0 | 48 | 6552, 6600 | 76 | 24 | 0 |
| 6601-6700 | 10 | 0 | 36 | 6624, 6660 | 73 | 27 | 0 |
| 6701-6800 | 12 | 1 | 56 | 6720 | 76 | 24 | 0 |
| 6801-6900 | 12 | 0 | 48 | 6840 | 76 | 24 | 0 |
| 6901-7000 | 13 | 0 | 48 | 6930 | 74 | 26 | 0 |
| 7001-7100 | 9 | 0 | 48 | 7020 | 76 | 24 | 0 |
| 7101-7200 | 10 | 0 | 54 | 7200 | 74 | 26 | 0 |
| 7201-7300 | 11 | 0 | 40 | 7280 | 74 | 26 | 0 |
| 7301-7400 | 9 | 0 | 48 | 7392 | 76 | 24 | 0 |
| 7401-7500 | 11 | 0 | 42 | 7488 | 75 | 25 | 0 |
| 7501-7600 | 15 | 0 | 64 | 7560 | 73 | 27 | 0 |
| 7601-7700 | 12 | 0 | 40 | 7680 | 76 | 24 | 0 |
| 7701-7800 | 10 | 0 | 48 | 7800 | 77 | 23 | 0 |
| 7801-7900 | 10 | 0 | 36 | 7812, 7840 | 75 | 25 | 0 |
| 7901-8000 | 10 | 0 | 60 | 7920 | 74 | 26 | 0 |
| 8001-8100 | 11 | 0 | 48 | 8064 | 72 | 28 | 0 |
| 8101-8200 | 10 | 0 | 48 | 8160, 8190 | 78 | 21 | 1 |
| 8201-8300 | 14 | 0 | 48 | 8280 | 74 | 26 | 0 |
| 8301-8400 | 9 | 0 | 60 | 8400 | 77 | 23 | 0 |
| 8401-8500 | 8 | 0 | 40 | 8424 | 73 | 27 | 0 |
| 8501-8600 | 12 | 0 | 48 | 8568, 8580 | 74 | 26 | 0 |
| 8601-8700 | 13 | 0 | 56 | 8640 | 78 | 22 | 0 |
| 8701-8800 | 11 | 0 | 48 | 8736 | 75 | 25 | 0 |
| 8801-8900 | 13 | 0 | 54 | 8820 | 75 | 25 | 0 |
| 8901-9000 | 9 | 0 | 48 | 9000 | 76 | 24 | 0 |
| 9001-9100 | 11 | 0 | 50 | 9072 | 76 | 24 | 0 |
| 9101-9200 | 12 | 0 | 48 | 9120, 9180 | 73 | 27 | 0 |
| 9201-9300 | 11 | 0 | 64 | 9240 | 74 | 26 | 0 |
| 9301-9400 | 11 | 0 | 60 | 9360 | 75 | 25 | 0 |
| 9401-9500 | 15 | 0 | 48 | 9450 | 75 | 25 | 0 |
| 9501-9600 | 7 | 0 | 48 | 9504, 9576, 9600 | 75 | 25 | 0 |
| 9601-9700 | 13 | 0 | 48 | 9660 | 76 | 24 | 0 |
| 9701-9800 | 11 | 0 | 48 | 9720 | 73 | 27 | 0 |
| 9801-9900 | 12 | 0 | 54 | 9900 | 78 | 22 | 0 |
| 9901-10000 | 9 | 0 | 40 | 9936 | 77 | 23 | 0 |
Немає коментарів:
Дописати коментар