Арифметична прогресія

Арифмети́чна прогре́сія це послідовність дійсних чисел виду

${\displaystyle a_{1},\ a_{1}+d,\ a_{1}+2d,\ \ldots ,\ a_{1}+(n-1)d,\ \ldots }$

де ${\displaystyle a_{1}}$ — це перший член прогресії, ${\displaystyle d}$ — це фіксована різниця між попереднім та наступним.

Приклади: а) 2, 4, 6,  8, ..... - це арифметична прогресія, що утворена множиною парних чисел( різниця дорівнює 2)

 б) 1, 3, 5, 7, ..... - це арифметична прогресія, що утворена множиною непарних чисел( різниця дорівнює 2)

 в) 6, 12, 18, 24, ..... - це арифметична прогресія, що утворена множиною натуральних чисел, які діляться націло на 6( різниця дорівнює 6).

 в) -0,6, -1,2, -1,8, -2,4, ..... - це арифметична прогресія, що утворена множиною від'ємних раціональних чисел, ( різниця дорівнює -0,6).

Формула для знаходження ${\displaystyle n}$-го члена прогресії:

${\displaystyle a_{n}=a_{1}+(n-1)d,\quad \forall n\geqslant 1}$

Для усіх членів прогресії, починаючи з другого, справедлива рівність:

${\displaystyle a_{n}=a_{n-1}+d\quad }$

Сума ${\displaystyle n}$ перших членів арифметичної прогресії може бути виражена такими формулами:

${\displaystyle S_{n}=\sum _{i=1}^{n}a_{i}={a_{1}+a_{n} \over 2}n={2a_{1}+d(n-1) \over 2}n}$.

Сума ${\displaystyle n}$ послідовних членів арифметичної прогресії починаючи з члена ${\displaystyle k}$:

${\displaystyle S_{n}={a_{k}+a_{k+n-1} \over 2}n}$;

Сума перших ${\displaystyle n}$ натуральних чисел:

${\displaystyle 1+2+\cdots +n={\frac {n(n+1)}{2}}}$.

Ця формула відома як трикутне число.

Існує історія про те, як Карл Ґаус відкрив цю формулу, коли навчався у третьому класі. Щоб подовше зайняти дітей, вчитель попросив клас порахувати суму перших ста чисел — 1+2+...+99+100. Ґаус помітив, що попарні суми з протилежних кінців однакові: 1 + 100 = 101, 2 + 99 = 101 і т. д., і тому зміг відразу відповісти, що сума дорівнює 5050. Дійсно, легко бачити, що рішення зводиться до формули ${\displaystyle {\frac {n(n+1)}{2}}}$, тобто до формули суми перших n чисел натурального ряду.

Також арифметична прогресія відноситься до такого розділу з математики, як комбінаторика

Завдання.

1.    Знайти суму всіх натуральних чисел, починаючи з одиниці, та закінчуючи числом 1000.

2.    Три числа, сума яких дорівнює 21, становлять арифметичну прогресію.  Якщо до них відповідно додати 2, 3 і 9, то утворені числа становитимуть геометричну прогресію.  Знайдіть ці числа.

3.    Знайдіть перший і п’ятий член арифметичної прогресії , якщо різниця її дорівнює 7, а сума шести її перших членів дорівнює 159.

4.    Третій член арифметичної прогресії становить 50% від шостого члена цієї прогресії, а їх добуток дорівнює 288.  Знайдіть другий член прогресії.

5.    Перший член арифметичної прогресії дорівнює 1, а її різниця дорівнює 3.  Знайти суму цієї прогресії.

6.    Між числами 1 та 8 вставте чотири числа так, щоб всі шість чисел утворювали арифметичну прогресію.

7.    Четвертий член арифметичної прогресії становить 25% від шостого члена цієї прогресії, а сума другого та п’ятого членів прогресії дорівнює 216.  Знайдіть суму перших чотирьох членів прогресії.

8.    Між числами 2 та 6,75 вставте два числа так, щоб всі чотири числа утворили арифметичної прогресію.

9.    Середнє арифметичне двох чисел дорівнює 10, а середнє арифметичне трьох дорівнює 6.  Знайдіть ці числа.

10.   Знайти перший і п’ятий член арифметичної прогресії, якщо її рызниця дорівнює 3, а сума шести її перших членів дорівнює 1820.

11.    Між числами 1 і 10 вставити два числа, кожне з яких буде середнім арифметичним  двох сусідніх чисел.

Арифметичну прогресію простих чисел являє собою набір простих чисел виду 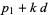 для фіксованих 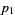і 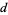  і послідовний 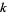, тобто 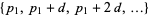. Наприклад, 199, 409, 619, 829, 1039, 1249, 1459, 1669, 1879, 2089 10 членів арифметичної прогресії простих чисел з різницею 210 а.

Він вже давно висловив припущення, що існують як завгодно довгі послідовності простих чисел в арифметичній прогресії (Guy 1994). Уже в 1770 році, і Лагранж Уорінг досліджували, наскільки велика загальна різниця арифметичної прогресії 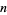повинні бути простими числами. У 1923 році Харді і Літтвуда (1923) зробив дуже загальну гіпотезу , відому як K -кратної гіпотези про розподіл простих сузір'їв , який включає в себе гіпотезу про те, що існує нескінченно довгі прості арифметичні прогресії , як окремий випадок. Важлива додаткова теоретична прогрес згодом була зроблена Ван дер Корпут (1939), який довів , ніж нескінченно багато трійок простих чисел в арифметичній прогресії, і Хис-Брауна (1981), який довів , що існує нескінченно багато чотирьох довгострокових прогресій , що складаються з три прості числа і число , яке є або простим або напівпервинне .

Тим НЕ менше, незважаючи на все це праця, доквеження загального результату при як завгодно довгих послідовностей простих чисел залишається відкритою гіпотеза (Guy 1994 стор. 15). Завдяки новій роботі Бен Грін і Теренс Тао, гіпотеза, здається, нарешті - то було вирішено в позитивному напрямі. У нещодавно опублікованому в препринті, Грін і Тао (2004) використовувати важливий результат , відомий як теорема Семереді в поєднанні з недавній роботі Голдстон і Йилдирим, розумний «принцип перенесення» і 48 сторінок щільних і технічних викладок зматематики, по- видимому , встановити основна теорема про те , що прості числа дійсно містять арифметичних прогресій довжини 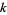для всіх 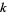(Weisstein 2004). Доказ, однак, є неконструктивним .

Нехай 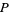зростаюча арифметична прогресія  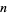простих чисел з мінімальною різницею 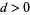. Якщо початковий елемент  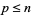 не поділяє 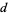, то елементи  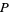повинні взяти на себе всі відрахування по модулю 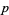, в зокрема, який - то елемент 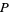повинен бути кратним 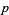. Так як 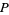містить тільки прості числа, то цей елемент має дорівнювати .

Нехай число простих чисел виду  менше , ніж позначати . Потім

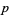(1)

де є логарифмічний інтеграл і є функцією totient .

Нехай 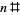позначимо primorial з 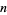. Тоді , якщо 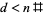деякі прем'єр 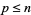не поділяє 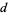, і що прем'єр 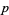в 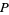. Таким чином, для того , щоб визначити , є чи 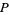має 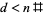, необхідно лише , щоб перевірити кінцеве число можливих 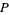(ті , з 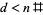і містить штрихом 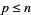) , щоб побачити , якщо вони містять тільки прості числа. Якщо немає, то 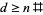. Якщо 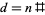, то елементи 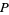не можуть бути зроблені , щоб покрити всі залишки будь-якого простого 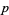. В K -кратної гіпотеза , то стверджує , що існує нескінченно багато арифметичних прогресій простих чисел з різницею .

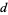Обчислення показує , що найменша можлива загальна різниця для набору 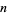 або більш простих чисел в арифметичній прогресії для 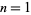, 2, 3, ... 0, 1, 2, 6, 6, 30, 150, 210, 210, 210, 2310 , 2310, 30030, 30030, 30030, 30030, 510510, ... (OEIS A033188 , Ribenboim 1989, Дабнер і Нельсон , 1997). Значення до 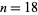суворі, в той час як інші є нижні межі , які передбачають справедливість K -кратної гіпотези і просто наведені 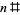. Найменші перші члени арифметичних прогресій 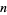простих чисел з мінімальними відмінностями є 2, 2, 3, 5, 5, 7, 7, 199, 199, 199, 60858179, 14933623, +147692845283, +834172298383, ... (OEIS A033189 ; Wilson) ,

Менші перші доданки можливі немінімально 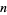-TERM прогресій. Приклади включають в себе 8 перспективі прогресії 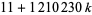для 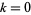, 1, ..., 7, 12 перспективі прогресії 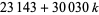для 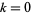, 1, ..., 11 (Голубєв 1969 Guy 1994), і арифметичній прогресії 13-термін  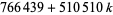для 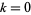, 1, ..., 12 (Guy 1994).

У наступній таблиці наведено найбільші відомі арифметичних прогресій 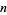простих чисел для малих 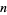, де

(2)

	прості числа для , 1, ...,	цифри	посилання
3		137514	J. К. Андерсон і ін. (2007)
4		11961	К. Девіс (2008)
5		6913	Д. Бродхерст (2008)
6		1606	К. Девіс (2006)
7		1290	К. Девіс (2006)
8		1037	П. Андервуд (2003)
9		401	М. Оукс (2006)

Більш повна таблиця підтримується Андерсена.

Найменша послідовність з шести послідовних простих чисел в арифметичній прогресії є

(3)

для 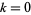, 1, ..., 5 (Lander і Паркін 1967 Дабнер і Нельсон , 1997).

Найбільший відомий випадок трьох послідовних простих чисел в арифметичній прогресії є 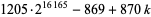для 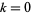, 1, 2, знайдена Т. Альм, Х. Rosenthal, J. К. Андерсен і Р. Ballinger в 2003 році.

Найбільша відома послідовність послідовних простих чисел в арифметичній прогресії (тобто всі числа між першим і останнім членом у прогресії, для членів , крім самих себе, є складовими) десять, дається

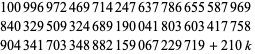(4)

для 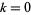, 1, ..., 9 (OEIS A033290 ), виявив Харві Dubner, Тоні Forbes, Манфреда Toplic, і ін. 2 березня 1998 р У відповідності з Дабнер і ін., Трильйон-кратне збільшення швидкості комп'ютера необхідно перш , ніж пошук послідовності з 11 послідовних простих чисел є практичним, тому вони очікують , що запис десять-простих чисел , щоб стояти в протягом тривалого часу приходити.

Це б'є рекорд дев'яти послідовних простих чисел, встановлений на 15 січня 1998 року тими ж дослідниками,

(5)

для 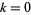, 1, ..., 8 (дві послідовності дев'яти нині відомі), прогресування восьми послідовних простих чисел , задається

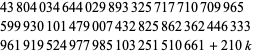(6)

для 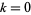, 1, ..., 7, виявив Харві Dubner, Тоні Forbes, і ін. 7 листопада 1997 (деякі з них в даний час відомі), і прогресуванню семи заданої

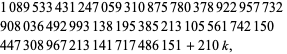(7)

для 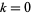, 1, ..., 6, відкрив Г. Dubner і Г. К. Нельсон на 29 серпня 1995 (Peterson 1995 року, Dubner і Нельсон , 1997).