Магічний куб

Ідеальний магічний куб являє собою чарівний кубик , для яких рядки, колони, стовпці, прошарки, просторових діагоналей, і діагоналей кожної


Існує тривіальне досконалий магічний куб порядку один, але не існує досконалих кубів для замовлень 2-4 (Schroeppel 1972; Benson та Якобі 1981, С. 23-25 ;. Gardner 1988). У той час як нормальні вчинені магічні куби замовлень 7 і 9 були відомі з кінця 1800 - х років, він довгий час невідомо , якщо ідеальних магічних кубиків замовлень 5 або 6 могли б існувати (Wells 1986, стор. 72), хоча Schroeppel (1972) і Гарднер (1988) відзначають , що будь-який такий кубик повинен мати центральне значення 63. (Смутно, Бенсона і Джейкоби (1981, стор. 5) наведемо таблицю , яка містить запис "
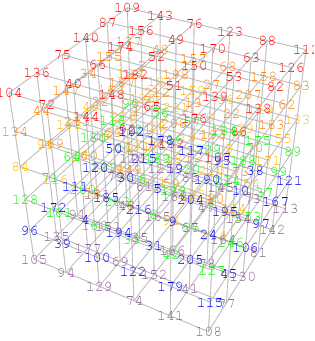
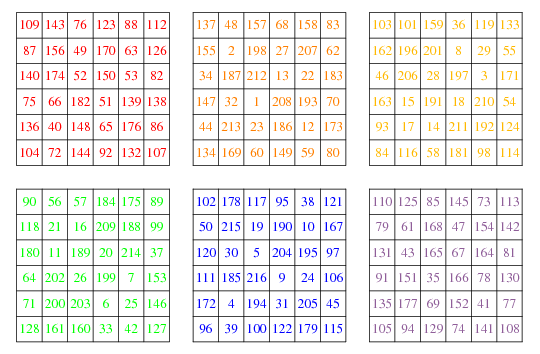
Бойєр і відкриття Трампа уважно стежив за відкриття Трампа першої відомої досконалої магії 6-го порядку на 1 вересня 2003 року (Boyer), було показано вище.

Перший опублікований досконалий магічний куб був порядок 7 куб знайшов преподобний А. Х. Фрост коледжу Сент - Джонс, Кембридж (Frost 1866 г.). Тому що Мороз був місіонером в Насик, Індія, він назвав особливий тип магічного куба він побудував куб Назік . Лангман (1962) згодом побудував ще один ідеальний чарівний кубик близько семи років , і все ще інші були знайдені Р. Schroeppel і Ернст Страус (Wells 1986, стор. 72).

Перший опублікований досконалий куб близько 8 був побудований Густава Франкенштейна і опубліковані в 11 березня 1875 року видання The Cincinnati Commercial газети (Barnard 1888 Гарднер 1976, Бенсон та Якобі 1981, Gardner 1988; Boyer). Зростаючий поетична на його відкритті, Франкенштейн продовжував відзначати "Це відкриття дає мені більше задоволення , ніж якби я знайшов золоту жилу під моїми дверима-підвіконня, і це насолода , як це робить бідність солодше , ніж багатство Креза." Будівництво близько 8 вчиненого магічного куба обговорюється в Болл і Кокстера (1987). Россер і Уокер знову відкрили порядок вісім куб в кінці 1930 - х років , але не опублікував його, і Майерс незалежно один від одного виявили куб , показаний вище в 1970 році (Wells 1986, стор 72 ;. Gardner 1988).
Frost (1878) знайшов ідеальний чарівний кубик близько 9, але це не використовувати послідовні номери. Перший опублікований нормальний досконалий куб порядку 9 був знайдений Планком (1905). Перший досконалий куб близько 10 був побудований його в 1988 році Лі Вень і доведені до С. Бойєр в грудні 2003. Ідеальні магічні куби замовлень 11 і 12, також відомі (Barnard 1888 року, Benson 1981, Boyer). У наступній таблиці наведено відомі вчинені куби і їх відкривачів (Boyer).
| посилання | |
| 3 | неможливо |
| 4 | неможливо (Schroeppel 1972) |
| 5 | Трамп і Бойєр (Boyer, Weisstein 2003) |
| 6 | Козир (Бойєр, Weisstein 2003) |
| 7 | Frost (1866 г.) |
| 8 | Франкенштейн (1875 г.) |
| 9 | Планка (1905) |
| 10 | Чи Вень (1988, Бойєр) |
| 11 | Барнард (1888 г.) |
| 12 | Бенсон (1981) |
Магічні квадрати
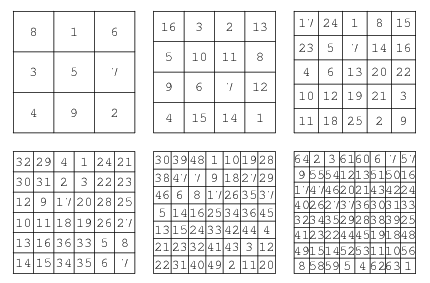
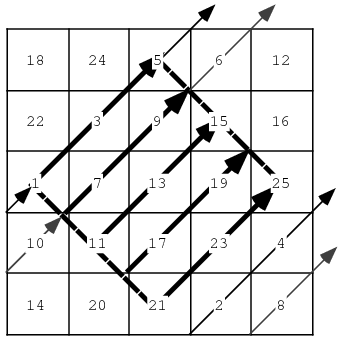

Addition-Multiplication Magic Square, Alphamagic Square, Antimagic Square, Associative Magic Square, Bimagic Square, Border Square, Dürer's Magic Square, Euler Square, Franklin Magic Square, Gnomon Magic Square, Heterosquare, Latin Square, Magic Circles, Magic Constant, Magic Cube, Magic Hexagon, Magic Labeling, Magic Series, Magic Tesseract, Magic Tour, Multimagic Square, Multiplication Magic Square, Panmagic Square, Semimagic Square, Talisman Square, Templar Magic Square, Trimagic Square
Немає коментарів:
Дописати коментар