Приклад рекусивної послідовності Фібоначчі

У XIII столітті італійський математик Фібоначчі розв'язував таку задачу:

Фермер годує кроликів. Кожен кролик народжує одного кролика, коли йому стає 2 місяці, а потім дає потомство в 1 кролик кожен місяць. Скільки кроликів буде у фермера через n місяців, якщо спочатку у нього був лише один (вважаємо, що кролики не гинуть і кожен народжений дає потомство за вище описаною схемою)?

Очевидно, що першого та другого місяця у фермера залишається один кролик, оскільки потомства ще немає. На третій місяць буде два кролики, оскільки перший через два місяці народить другого кролика. На четвертий місяць перший кролик дасть ще одного, а другий кролик потомства не дасть, оскільки йому ще тільки один місяць. Отже на четвертий місяць буде три кролики.

Можна помітити, що кількість кроликів після n — го місяця дорівнює кількості кроликів, які були у n — 1 місяці плюс кількість народжених кроликів. Останніх буде стільки, скільки є кроликів що дають потомство, або дорівнює кількості кроликів, яким вже виповнилося 2 місяці (тобто кількості кроликів після n — 2 місяця).

Якщо через F_n позначити кількість кроликів після n — го місяця, то має місце таке рекурентне співвідношення:

F_n = F_n-1 + F_n-2, F₁ = F₂ = 1

Покладемо F₀ = 0, при цьому співвідношення при n = 2 залишиться істинним. Таким чином утворюється послідовність

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … ,

Послідовність  Фібоначчі можна продовжити у зворотному напрямі.

Як це зробити? Перед нулем стоїть невідомий елемент х, згідно рекурсивній формулі:

F(-1)+0=1, Отже, перед нулем займає своє місце 1. Далі продовжимо.

 F(-2)= 0-1= -1,  

F(-3)= 1-(-1)=2

F(-4)= -1-2= -3

F(-5)= 2-(-3)= 5

F(-6)= -3-5=-8, і так далі.  Отримаємо продовжену вліво і вправо послідовність Фібоначчі:

 ...., -21, 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3,  5, 8, 13, 21, ....

Парні місця лівого краю стають від'ємними елементами. 

Послідо́вність Фібона́ччі, чи́сла Фібона́ччі — у математиці числова послідовність ${\displaystyle {F_{n}},}$ задана рекурентним співвідношенням другого порядку

${\displaystyle F_{1}=1,F_{2}=1,F_{n+2}=F_{n}+F_{n+1},n=1,2,3,\ldots ,}$

${\displaystyle F_{1}=1,F_{2}=1,F_{3}=2,F_{4}=3,F_{5}=5,F_{6}=8,F_{7}=13,F_{8}=21,\,}$

і т. д. Ця послідовність виникає у найрізноманітніших математичних ситуаціях — комбінаторних, числових, геометричних.

Простіше кажучи, перші два члени послідовності — одиниці, а кожний наступний — сума значень двох попередніх чисел:

${\displaystyle 1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}$

Часто, особливо в сучасному вигляді, послідовність доповнюється ще одним початковим членом:

${\displaystyle 0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\;\ldots \;}$.

З визначенням, перші два числа в послідовності Фібоначчі є або 1 і 1, або 0 і 1, в залежності від обраного початку послідовностей, а кожне наступне число є сумою двох попередніх.

В математичних термінах, послідовність чисел Фібоначчі F_n визначається як рекурентне співвідношення

${\displaystyle F_{n}=F_{n-1}+F_{n-2},}$

із початковими значеннями^[2][3]

${\displaystyle F_{1}=1,\;F_{2}=1}$

або^[4]

${\displaystyle F_{0}=0,\;F_{1}=1.}$

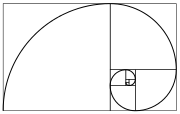
У природі числа Фібоначчі часто трапляються в різних спіральних формах. Так, черешки листя примикають до стебла по спіралі, що проходить між двома сусідніми листками: 1/3 повного оберту в ліщини, 2/5 — у дуба, 3/8 — у тополі і груші, 5/13 — у верби; лусочки на ялиновій шишці, насіння соняшника розташовані спіралями, причому кількості спіралей кожного напрямку також, як правило, числа Фібоначчі.

Послідовність названа на честь математика XIII століття Леонардо Фібоначчі з Пізи. Його 1202 книга Книга абака представила цю послідовність спільності західноєвропейських математиків,^[5], хоча така послідовність вже була описана раніше як числа Вараханка в Індійській математиці. Послідовність описана в Книзі абака починалася із F₁ = 1.

Властивості чисел Фібоначчі

• Найбільший спільний дільник двох чисел Фібоначчі дорівнює числу Фібоначчі з індексом, рівним найбільшому спільному дільнику індексів, тобто: ${\displaystyle (F_{m},F_{n})=F_{(m,n)}\,\!}$. Внаслідок цього:
  • ${\displaystyle F_{m}}$ ділиться на ${\displaystyle F_{n}}$ тоді й тільки тоді, коли ${\displaystyle m}$ ділиться на ${\displaystyle n}$ (за винятком ${\displaystyle n=2}$);
  • кожне третє число Фібоначчі парне (${\displaystyle F_{3}=2,F_{6}=8,F_{9}=34}$);
  • кожне четверте ділиться на три (${\displaystyle F_{4}=3,F_{8}=21,F_{1}2=144}$);
  • кожне п'ятнадцяте закінчується нулем (${\displaystyle F_{15}=610}$);
  • два сусідніх числа Фібоначчі взаємно прості;
  • ${\displaystyle F_{m}}$ може бути простим тільки для простих ${\displaystyle m}$ (за єдиним винятком ${\displaystyle m=4,}$ що пов'язано з ${\displaystyle F_{2}=1}$). Зворотне твердження невірне: ${\displaystyle F_{19}=4181=37\cdot 113,}$ хоча ${\displaystyle 19}$ — просте число. Тепер невідомо, чи існує нескінченно багато простих чисел Фібоначчі.
• Використовуючи те саме рекурентне співвідношення, що і на початку, у вигляді ${\displaystyle F_{n}=F_{n+2}-F_{n+1}}$, можливо поширити визначення чисел Фібоначчі і на від'ємні індекси: ${\displaystyle F_{0}=0,F_{-1}=1,F_{-2}=-1,F_{-3}=2,F_{-4}=-3,F_{-5}=5,\ldots .}$ Неважко переконатися, що ${\displaystyle F_{-n}=(-1)^{n+1}F_{n},}$ тобто одержуємо таку саму послідовність із знаками, що чергуються.
• Послідовність чисел Фібоначчі є частковим випадком генерованої послідовності, її характеристичний многочлен рівний ${\displaystyle x^{2}-x-1}$ й має корені ${\displaystyle \phi }$ і ${\displaystyle -1/\phi }$.
• Генератрисою послідовності чисел Фібоначчі є:

${\displaystyle 0+x+x^{2}+2x^{3}+3x^{4}+5x^{5}+\dots =\sum _{n=0}^{\infty }F_{n}x^{n}={\frac {x}{1-x-x^{2}}}}$

• Числа Фібоначчі можна представити значеннями континуант на наборі одиниць: ${\displaystyle F_{n}=K_{n}(1,\dots ,1)}$, тобто

${\displaystyle F_{n}=\det {\begin{pmatrix}1&1&0&\cdots &0\\-1&1&1&\ddots &\vdots \\0&-1&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &1\\0&\cdots &0&-1&1\end{pmatrix}}}$, а також ${\displaystyle \ F_{n+1}=\det {\begin{pmatrix}1&i&0&\cdots &0\\i&1&i&\ddots &\vdots \\0&i&\ddots &\ddots &0\\\vdots &\ddots &\ddots &\ddots &i\\0&\cdots &0&i&1\end{pmatrix}}}$,

де матриці мають розмір ${\displaystyle n\times n}$, ${\displaystyle i}$ — уявна одиниця.

• Для будь-якого n,

${\displaystyle {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n}={\begin{pmatrix}F_{n+1}&F_{n}\\F_{n}&F_{n-1}\end{pmatrix}}.}$

Ця формула надає швидкий алгоритм обчислення чисел Фібоначчі за допомогою матричного варіанта алгоритма швидкого піднесення до степеня. Обчислення визначників дає:

${\displaystyle (-1)^{n}=F_{n+1}F_{n-1}-F_{n}^{2}}$

• Відношення ${\displaystyle {\frac {F_{n+1}}{F_{n}}}}$ є підходящими дробами золотого перетину ${\displaystyle \phi }$ і, зокрема, ${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\phi }$.

Доведення. Позначимо ${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=x.}$ Враховуючи, що ${\displaystyle F_{n+1}=F_{n}+F_{n-1},}$ і вважаючи, що шукана границя існує і не дорівнює нулю, запишемо:

${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}=\lim _{n\to \infty }{\frac {F_{n}+F_{n-1}}{F_{n}}}=1+\lim _{n\to \infty }{\frac {F_{n-1}}{F_{n}}}=1+{\frac {1}{\lim _{n\to \infty }{\frac {F_{n}}{F_{n-1}}}}}=1+{\frac {1}{\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}}}.}$

Отримуємо просте рівняння ${\displaystyle x=1+{\frac {1}{x}},}$ яке зводиться до квадратичного рівняння ${\displaystyle x^{2}-x-1=0.}$

Розв'язками є числа ${\displaystyle x_{1}={\frac {1+{\sqrt {5}}}{2}}}$ і ${\displaystyle x_{2}={\frac {1-{\sqrt {5}}}{2}}.}$

Очевидно, що розв'язок ${\displaystyle x_{2}<0}$ не підходить, тому остаточно:

${\displaystyle \lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}={\frac {1+{\sqrt {5}}}{2}}=\phi .}$

• Суми біноміальних коефіцієнтів на діагоналях трикутника Паскаля є числами Фібоначчі з огляду на формулу

${\displaystyle F_{n+1}=\sum _{k=0}^{\lfloor n/2\rfloor }{n-k \choose k}}$.

• У 1964 р. J. H. E. Cohn довів, що єдиними точними квадратами серед чисел Фібоначчі є ${\displaystyle F_{0}=0,F_{1}=F_{2}=1}$ і ${\displaystyle F_{12}=144=12^{2}.}$

• Множина чисел Фібоначчі збігається з множиною натуральних значень наступного полінома двох змінних

${\displaystyle P(x,y)=2xy^{4}+x^{2}y^{3}-2x^{3}y^{2}-y^{5}-x^{4}y+2y,}$

де ${\displaystyle x,y\in \mathbb {Z} }$ — цілі числа, див. P. Ribenboim, The New Book of Prime Number Records, Springer, 1996, стор. 153. Цей факт, знайдений Дж. Джоунзом, відіграє ключову роль у теоремі Матиясевича (негативному розв'язанні десятої проблеми Гільберта), тому що він надає спосіб задати експоненціально зростаючу послідовність чисел Фібоначчі у вигляді діофантової множини.

В математиці, послідовностями Люка називають сімейство пар лінійних рекурентних послідовностей другого порядку, вперше розглянутих Едуардом Люка.

Послідовності Люка являють собою пари послідовностей ${\displaystyle \{U_{n}(P,Q)\}}$ и ${\displaystyle \{V_{n}(P,Q)\}}$, що задовольняють одному і тому ж рекурентному співвідношенню з коефіцієнтами P і Q:

${\displaystyle U_{0}(P,Q)=0,\quad U_{1}(P,Q)=1,\quad U_{n+2}(P,Q)=P\cdot U_{n+1}(P,Q)-Q\cdot U_{n}(P,Q),\,n\geq 0}$

${\displaystyle V_{0}(P,Q)=2,\quad V_{1}(P,Q)=P,\quad V_{n+2}(P,Q)=P\cdot V_{n+1}(P,Q)-Q\cdot V_{n}(P,Q),\,n\geq 0}$

Приклади

Деякі послідовності Люка носять власні імена:

• ${\displaystyle \{U_{n}(1,-1)\}}$ - числа Фібоначчі
• ${\displaystyle \{V_{n}(1,-1)\}}$ - числа Люка 
• Числа Люка задаються рекурентною формулою

• ${\displaystyle L_{n}=L_{n-1}+L_{n-2}}$

  із початковими значеннями ${\displaystyle L_{0}=2}$ и ${\displaystyle L_{1}=1}$.
  Послідовність чисел Люка починається так:

  2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, …

• ${\displaystyle \{U_{n}(2,-1)\}}$ - числа Пелля
• ${\displaystyle \{V_{n}(2,-1)\}}$ - числа Пелля-Люка
• ${\displaystyle \{U_{n}(3,2)\}}$ - числа Мерсенна   
• Число́ Мерсе́нна (Mersenne number) — числа виду , де  — натуральне число. Числа називають іменем французького математика Марена Мерсенна, що жив на початку XVII століття.
  Послідовність чисел Мерсенна починається так:

  1, 3, 7, 15, 31, 63, 127, 255, 511, 1023,

• ${\displaystyle \{U_{n}(1,-2)\}}$ - числа Якобшталя

Явні формули

Характеристичним многочленом послідовностей Люка ${\displaystyle \{U_{n}(P,Q)\}}$ та ${\displaystyle \{V_{n}(P,Q)\}}$ є:

${\displaystyle x^{2}-P\cdot x+Q}$

Його дискримінант ${\displaystyle D=P^{2}-4Q}$ вважається не рівним нулю. Корені характеристичного многочлена

${\displaystyle \alpha ={\frac {P+{\sqrt {D}}}{2}}}$ и ${\displaystyle \beta ={\frac {P-{\sqrt {D}}}{2}}}$

можна використовувати для отримання явних формул:

${\displaystyle U_{n}(P,Q)={\frac {\alpha ^{n}-\beta ^{n}}{\alpha -\beta }}={\frac {\alpha ^{n}-\beta ^{n}}{\sqrt {D}}}}$

та

${\displaystyle V_{n}(P,Q)=\alpha ^{n}+\beta ^{n}.~}$

Формула Біне

Числа Фібоначчі тісно пов'язані з золотим перетином ${\displaystyle \phi ={\frac {1+{\sqrt {5}}}{2}}.}$ Формула Біне виражає за допомогою ${\displaystyle \phi }$ значення ${\displaystyle F_{n}}$ в явному вигляді як функцію від ${\displaystyle n}$:

${\displaystyle F_{n}={\frac {\phi ^{n}-(-\phi )^{-n}}{\phi -(-\phi )^{-1}}}={\frac {\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}}{\sqrt {5}}}\approx {\frac {\phi ^{n}}{\sqrt {5}}}\quad (n\geqslant 1).}$

При цьому ${\displaystyle \phi =1,618\ldots \,\!}$ і ${\displaystyle (-\phi )^{-1}=1-\phi =-0,618\ldots \,\!}$ є коренями квадратного рівняння ${\displaystyle x^{2}-x-1=0\,\!}$.

Оскільки ${\displaystyle -1<1-\phi <0,}$ знаходимо, що при ${\displaystyle n\geqslant 1,\ -1<(1-\phi )^{n}<1.}$ Тому з формули Біне випливає, що для всіх натуральних ${\displaystyle n,\,F_{n}}$ є найближчим до ${\displaystyle {\frac {\phi ^{n}}{\sqrt {5}}}\,}$ цілим числом, тому ${\displaystyle F_{n}=\left[{\frac {\phi ^{n}}{\sqrt {5}}}\right]}$ або ${\displaystyle F_{n}=\left\lfloor {\frac {\phi ^{n}}{\sqrt {5}}}+{\frac {1}{2}}\right\rfloor }$. Зокрема, справедлива асимптотика ${\displaystyle F_{n}\sim {\frac {\phi ^{n}}{\sqrt {5}}},\ n\to \infty .}$